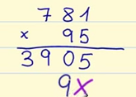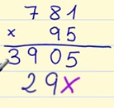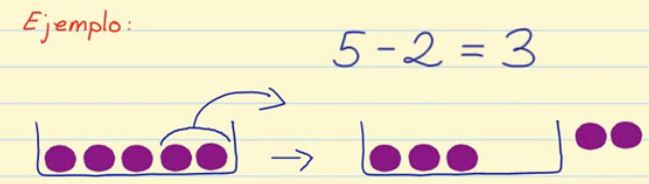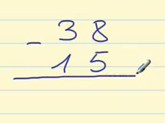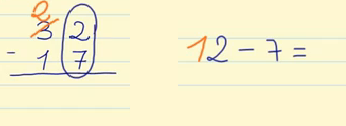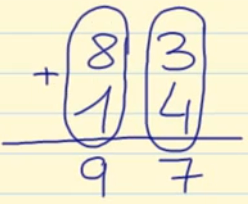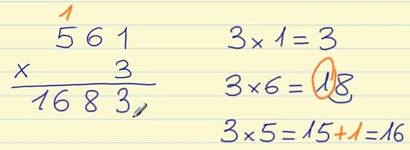Las divisiones son, junto a las sumas, restas y multiplicaciones, operaciones matemáticas que realizamos frecuentemente en nuestra vida cotidiana.
Veremos en este artículo cómo se hacen las divisiones, su significado. También estudiaremos los criterios de divisibilidad y conoceremos cómo hacer la prueba de la división para saber si la hemos resuelto bien.
Divisiones
Lo primero que debemos saber es qué es una división. Una división se trata de un reparto en partes iguales. Pongamos un ejemplo:
Hay una bolsa con 10 canicas y 5 amigos. Quieren repartir las canicas de modo que todos tengan la misma cantidad de ellas. Uno de los amigos coge la bolsa y empieza a dar una canica a cada uno y sí mismo hasta que se acaban. Cuando finaliza el reparto, cada uno de los amigos ha conseguido 2 canicas. De esto podemos deducir que 10 canicas divididas entre 5 amigos es igual a que cada amigo tenga dos canicas.
Si expresamos matemáticamente el ejemplo anterior, tan solo diríamos que 10 dividido entre 5 es igual a 2.
Pongamos otro ejemplo, un poquito más difícil. Ahora tenemos que repartir 125 caramelos entre los mismos cinco amigos. Se podría repartir uno a uno cada caramelo entre cada amigo pero, en este caso, ¡hay un montón de caramelos! Así que lo mejor será aprender a dividir, así sabremos rápidamente que cada amigo tocará a 25 caramelos. La división en este caso, se expresaría así:

Y, al resolverla, nos daría que cada uno de los amigos tocan a 25 caramelos. La división terminada, tendría este aspecto:
No te preocupes si aún no entiendes cómo hemos desarrollado esta división, más adelante te explicamos todo, paso a paso.
Partes de la división
Los términos o partes de la división son, el cociente y del resto, el dividendo y el divisor. Los términos dan lugar a las llamadas divisiones de una cifra (divisor con un solo dígito), divisiones de dos cifras (divisores de dos dígitos), divisiones con decimales en el dividendo y/o en el divisor, etc.
Veamos cada parte, una a una:
- Partes de la división:
- Dividendo: Es el número que hay que repartir. Para el ejemplo de la imagen, este número es el 125 que representan los caramelos.
- Divisor: Es el número entre el cual se divide el dividendo, es decir, las partes entre las que hay que repartir. Para nuestro ejemplo, este es el número 5 que representa a los cinco amigos entre los que hay que repartir los 125 caramelos.
- Cociente: Es el resultado de la división. En nuestro ejemplo, 25. Es decir, cada amigo toca a 25 caramelos.
- Resto: Es el número que sobra cuando se termina de hacer la división. Este número puede ser cero u otro número, pero siempre tiene que ser menor que el divisor. Representa la parte que no puede repartirse. En nuestro ejemplo, el resto es 0 porque hemos podido repartir todos los caramelos.
Divisiones de una cifra
Veamos ahora cómo se divide. Empezaremos haciendo divisiones de una sola cifra en el divisor. Seguiremos con el mismo ejemplo de antes, es decir, vamos a dividir 125 entre 5. Cuando comenzamos a estudiar las divisiones hay dos formas de resolverlas: con resta o sin ella. Vamos a ver el procedimiento de cada una de ellas.
Divisiones de una cifra con resta
Empezamos escribiendo la división.
Ahora tenemos que ver cuántas cifras tenemos que usar del dividendo para dividir por el divisor. La norma que hay que seguir siempre es que el número del dividendo que vamos a dividir debe ser igual o mayor al del divisor. Por ejemplo, en 125 no podemos empezar dividiendo 1 entre 5 porque 1 es menor que 5, así que cojo el siguiente número del dividendo. Ahora tengo el número 12 ¿es mayor que cinco? sí, así que ya puedo dividir.

Ahora tenemos que calcular mentalmente qué número multiplicado por el divisor (5) se acerca más al dividendo (12) sin pasar a éste. Es decir, ¿qué número multiplicado por 2 se acerca más a 12 sin sobrepasarlo? Veamos, 5 x1 = 5, 5×2= 10, 5×3 =15 No podemos utilizar el 3 porque al multiplicarlo por 5 supera a 12, tampoco podemos utilizar el 1 porque al multiplicar por dos nos acercamos más a 12, puesto que 10 está mucho más cerca de 12 que 5. Así pues, ya sabemos que debemos multiplicar por 2. Anotamos 2 en el cociente y ponemos la multiplicación debajo del dividendo, en nuestro caso, 10.
Lo siguiente que debemos hacer es la resta de 12 menos 10 y anotar el resultado debajo. Para nuestro ejemplo, 2.
Debemos seguir con la división ya que nos falta parte del dividendo por hacer. Pasamos el siguiente número del dividendo (el 5) al lado del dos que teníamos y volvemos a hacernos la misma pregunta. Ahora sería, ¿qué número multiplicado por 5 se acerca más a 25? ¡qué fácil! en este caso es el 5, puesto que 5 x 5 =25. Anotamos el cinco en el cociente detrás del 2 y escribimos 25 debajo del 25 que ya teníamos.
Ya solo nos queda hacer la resta final, 25 menos 25 es igual a 0, que es el resto de nuestra división. También podemos deducir con esto que 125 dividido entre 5 es igual 25.
Divisiones de una cifra sin resta
Una vez se manejan bien las divisiones con resta ya estamos preparados para hacerlas sin ella. Este es un proceso mental que poco a poco iremos dominando para hacer así todas nuestras divisiones. Seguiremos con el mismo ejemplo para que puedas ver las diferencias. Lo primero, es escribir la división:
El siguiente paso también es igual. Cogemos el número del dividendo que sea mayor o igual al divisor, en nuestro caso 12. La pregunta es la misma también ¿qué número multiplicado por 5 se acerca más a 12? La respuesta es 2, así que escribimos un 2 en el cociente. Ahora viene la diferencia, restamos de cabeza sin anotarlo. Es decir 5 por 2 es igual a 10, 12 menos 10 es igual a 2, así que solo colocamos el 2 debajo del 12.
Ahora debemos seguir con el siguiente número del dividendo, así que anotamos el 5 al lado del 2.
Ahora nos preguntamos qué número multiplicado por 5 se acerca o igual a 25. La respuesta es 5. Anotamos este 5 en el cociente detrás del 2 y restamos mentalmente 25 menos 25 que es igual a 0. Anotamos ese 0 en el resto. ¡Ya la hemos resuelto! 125 entre 5 es igual a 25.
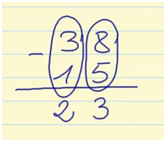
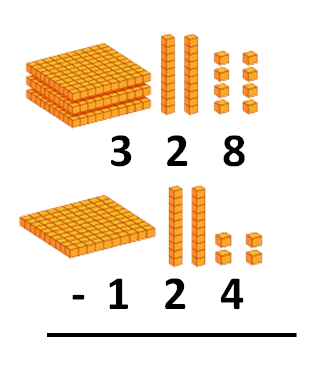
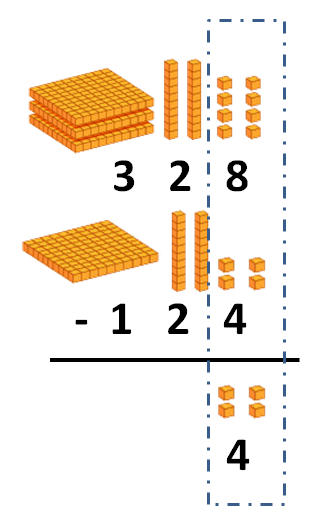
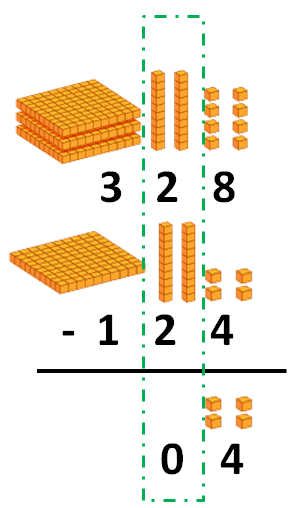
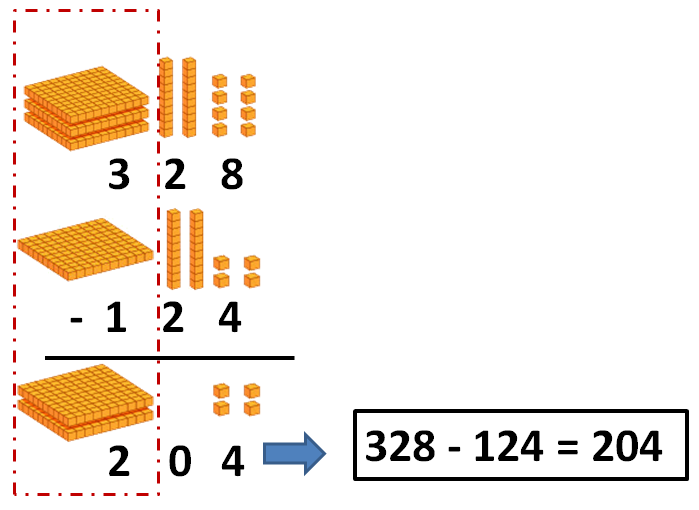
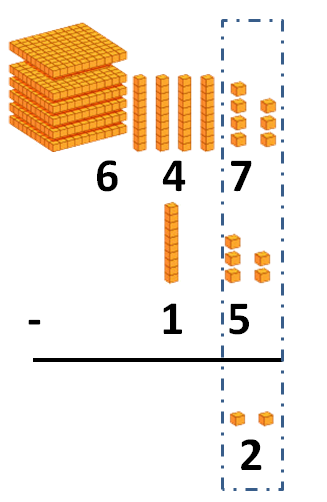
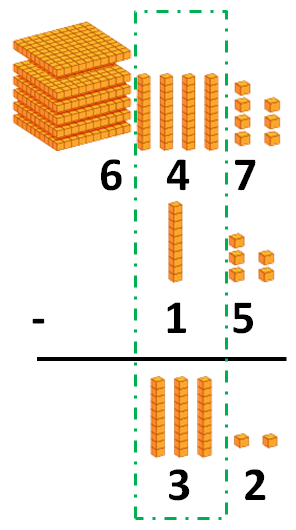
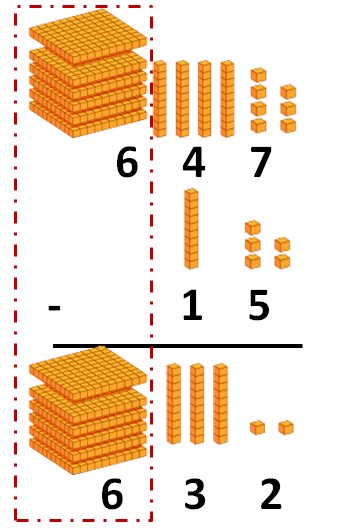
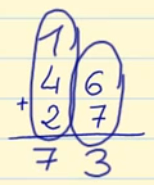
Puedes ver otros ejemplos de divisiones con y sin resta en la siguiente imagen:
Divisiones enteras y divisiones exactas
- Divisiones exactas: es cuando el resto es igual a 0. Es decir se ha podido repartir todo el dividendo en partes iguales.
- Divisiones enteras: es cuando al repartir nos sobra algo, esto es, no se ha podido dividir el dividendo entre el divisor en partes iguales. Sabemos que una división es entera cuando el resto es distinto de 0.
En la siguiente imagen puedes ver algunos ejemplo:
Divisiones de dos cifras
Vamos a ver ahora cómo resolver divisiones de dos cifras en el divisor, lo haremos sin resta, solo mentalmente. Para nuestro ejemplo dividiremos 4692 entre 24. Lo primero es anotar la división:
Ahora tenemos que seleccionar el número más pequeño del dividendo que sea mayor que el divisor. En nuestro caso este número sería el 46.
Y ahora nos preguntamos que número multiplicado por 24 se acerca más a 46 sin pasarse. En nuestro caso este número es el 1 que anotaremos en el cociente.
Multiplicamos 24 por 1 y lo restamos mentalmente a 26. Esto es 24 x 1 = 24 ; 46 – 24 = 22. Así pues anotamos 22 debajo de 46.
Ahora tenemos que seguir con el siguiente número del dividendo, el 9. Anotamos el 9 al lado del 22.
Tenemos que dividir 229 entre 24, buscamos el número que multiplicado por 24 se acerque más a 229, este número es el 9 que lo anotamos en el cociente a la derecha del 1. Y hacemos mentalmente lo siguiente: multiplicamos 9 x 4 = 36, cogemos el número de la unidades (6) y lo restamos al 9, el resultado es un 3 que colocamos debajo del 9. Ahora multiplicamos 9 x 2 = 18. A este 18 debemos sumarle el número de las decenas del 36 anterior; 18 + 3 = 21. Ahora restamos 22 de 21 y el 1 que nos sale lo colocamos a la izquierda del 3 anterior.
Ahora debemos añadir el último número del divisor, que es el 2. Lo anotamos a la derecha del 13.
Hacemos el mismo paso en ocasiones anteriores. En este caso el número que necesitamos es el 5 que anotamos a la derecha del cociente que llevamos.
Ya no tenemos más números en el dividendo y el resto es diferente de 0. Esto nos dice que la división no es exacta, podemos seguir dividiendo pero ya tendríamos que hacerlo añadiendo una coma decimal. Veamos cómo se hace. Debemos poner una coma decimal a la derecha del cociente y anotar un 0 a la derecha del 12 que nos ha quedado como resto.
Ahora dividiremos 120 entre 24 como ya sabemos. El número a apuntar en el cociente será el 5. El resto en este caso ya es igual a 0 por lo que esta división ha terminado. Si el resto fuese distinto de cero podríamos seguir sacando decimales añadiendo otro 0 al resto.
Puede suceder haciendo divisiones, que el número que queda en el resto sea más pequeño que el divisor pero aún queden números en el dividendo para anotar. Cuando pasa eso, debemos colocar en el cociente un 0 y bajar el siguiente número del divisor. A partir de ahí continuamos normalmente con la división. Veamos un ejemplo.
Vamos a dividir 408 entre 4. Lo primero anotamos la división:
Comenzamos la división, cogiendo el 4 del dividendo y dividiéndolo entre el 4 del divisor. Es fácil, el resultado que debemos anotar en el cociente es 1 y en el resto un 0.
Ahora debemos bajar el siguiente número del dividendo que es el 0.
Cuando sucede que el número a dividir es más pequeño que el divisor, debemos anotar un 0 en el cociente.
Anotamos el siguiente número del dividendo al lado del resto que tengamos. Ahora ya podemos dividir. 8 entre 4 es igual a 2.
Terminamos la división que quedaría así:
Prueba de la división
Existe una manera de saber si hemos resuelto bien una división. Es lo que se conoce como la prueba de la división. En la siguiente imagen verás las fórmula para hacerlo:
Hagamos la prueba de la división para este ejemplo:
Dividendo = divisor x cociente + resto
140 = 8 x 17 + 4
140 = 136 + 4
140 = 140
¡Correcto!
Criterios de divisibilidad
Los criterios de divisibilidad son unas instrucciones o guías que nos servirán como «truco» para saber si un número es divisible por otro. Es decir que un número al dividirlo por otro su resto sea 0 o dicha división sea exacta. Vamos a ver los criterios de divisibilidad para los números 2, 3, 4, 5, 6, 9 y 10.
- Criterios de divisibilidad
- Un número es divisible entre 2 si acaba en 0 o es una cifra par.
- 342 es divisible entre 2 porque es par.
- 270 es divisible entre 2 porque acaba en 0.
- 345 no es divisible entre dos porque no es par ni acaba en 0.
- Un número es divisible entre 3 si la suma de sus cifras es igual a 3 o a un múltiplo de 3.
- 21 es divisible entre 3 porque la suma de sus cifras es 3.
- 369 es divisible entre 3 porque la suma de sus cifras es un múltiplo de 3. 3+6+9 = 18 es un múltiplo de 3.
- Un número es divisible entre 4 si sus dos últimas cifras son 00 o un múltiplo de 4.
- 23400 es divisible entre 4 porque sus dos últimas cifras son 00.
- 14536 es divisible entre 4 porque sus dos últimas cifras, el 36, forman un múltiplo de 4. 4 x 9 =36
- Un número es divisible entre 5 si acaba en 5 o en 0.
- 2345645 es divisible entre 5 porque acaba en 5.
- 234890 es divisible entre 5 porque acaba en 0.
- Un número es divisible entre 6 si a su vez es divisible por 2 y por 3.
- 132 es divisible entre 6 porque es par (divisible entre 2) y la suma de sus cifras, 6, es un múltiplo de 3 (divisible entre 3).
- 30450 es divisible entre 6 porque termina en 0 (divisible entre 2) y la suma de sus cifras, 12, es un múltiplo de 3 (divisible entre 3).
- Un número es divisible entre 9 si la suma de sus cifras es igual a 9.
- 1242 es divisible entre 9 porque 1+2+4+2 = 9
- 200331 es divisible entre 9 porque 2+0+0+3+3+1 = 9
- Un número es divisible entre 10 si termina en 0.
- 125410 – 635210 – 785460 – 1250 – 420 – 90 son todos números divisibles entre 10 porque todos terminan en 0.