TIPS PARA APRENDER A RESTAR

La resta. Concepto y ejercicios para practicar

En este post vamos a aprender la resta.

Lo primero de todo, vamos a ver qué es la resta: Restar es quitar una cierta cantidad a otra que ya teníamos.

Por ejemplo: Si tenemos en una caja 5 bolas moradas, y sacamos de ésta 2 bolas, nos quedan dentro de la caja 3 bolas. Por lo tanto: 5 – 2 = 3

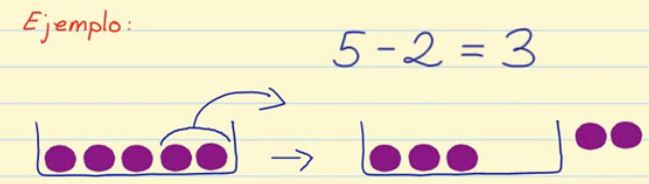
 Otro ejemplo de resta: Si tenemos 7 pasteles y nos comemos 1, ¿cuántos pasteles tendremos? 7 – 1 = 6

Ahora vamos a aprender a restar con los dedos. Si tenemos 9 dedos, 5 en una mano y 4 en la otra, y queremos restar 5 dedos, ¿cuántos dedos nos quedan? Escondemos los 5 dedos de una mano y contamos los que nos quedan. Nos quedan 4 dedos. Por lo tanto, 9 – 5 = 4.

Cómo hacer restas con y sin llevadas

Restas sin llevada

Los pasos que hay que seguir son:

• Coloca el sustraendo debajo del minuendo de manera que coincidan las unidades en la misma columna
• Resta cada columna por separado empezando por las unidades
• Escribe el resultado de la resta debajo de cada columna

Por ejemplo:

Vamos a hacer la resta: 38 – 15

38 es el minuendo y 15 es el sustraendo, por lo tanto, colocamos el 38 y debajo el 15, de manera que el 5 esté justo debajo del 8.

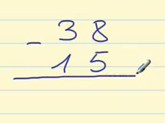
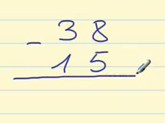
Empezamos restando la columna de las unidades:   8 – 5 = 3, y escribimos el 3 debajo de la columna de las unidades.

Ahora restamos la columna de las decenas:   3 – 1 = 2, y escribimos el 2 debajo de la columna de las decenas.

El resultado de restar 38 – 15 = 23

Restas con llevada

Cuando la cifra del minuendo es menor que la cifra del sustraendo tiene que pedir ayuda a la cifra del minuendo de la siguiente columna.

Por ejemplo:

Vamos a restar 32 – 17

Colocamos el 17 debajo del 32 de manera que coincidan las unidades en la misma columna, es decir, el 7 y el 2.

Empezamos restando la columna de las unidades:  2 – 7, pero como 2 es menor que 7  tenemos que pedir ayuda a la siguiente columna. Esta columna se quita una decena (3 – 1) para dar 10 unidades (2 + 10).

Ahora sí podemos restar  12 – 7 = 5

Restamos la columna de las decenas:  2 – 1 = 1

Por lo tanto, el resultado de la resta 32 – 17 = 15

Restas en vertical

vamos a repasar el material que utilizaremos para hacer las restas. ¿Cómo representamos un número con este material? ¡Muy fácil! Utilizaremos tantas unidades como corresponden al número, por ejemplo:

Y ¿para qué sirven las decenas? Para que sea más fácil representarla y no tengamos que utilizar unidades sueltas, las agrupamos en una barra que contiene 10 unidades:

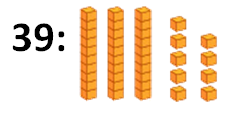
Además, hoy vamos a hacer restas que incluyen centenas. Para representar mejor una centena, utilizaremos una placa de 100 unidades (que contiene 10 barras de 10 unidades cada una). Por ejemplo:

Restas en vertical

Vamos a empezar a ver las restas en vertical. Para entenderlo mejor, vamos a resolver dos restas:

328 – 124

647 – 15

Vamos a comenzar con la primera. Veremos dos pasos: el primero consiste en colocar los términos de la resta y el segundo en hacer la resta.

1. Colocamos los términos

Para hacer una resta en vertical debemos asegurarnos de que hemos colocado correctamente sus términos. Para ello, debemos colocar en la línea de arriba el minuendo y justo debajo, el sustraendo. Cuando los colocamos, debemos alinear en la misma columna las unidades con las unidades, las decenas con las decenas, etc:

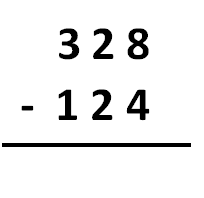
Para entender mejor cómo es, vamos a utilizar el material:

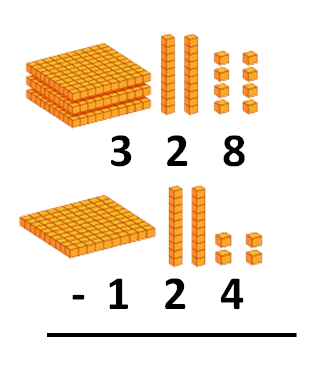
2. Hacemos la resta

Ahora tenemos que hacer la resta, teniendo en cuenta dos cosas muy importantes:

a) Siempre vamos a restar los números que hay en una misma columna

b) Empezamos por la columna de las unidades, y vamos avanzando por columnas hacia la izquierda

Así, primero restamos la columna de las unidades:

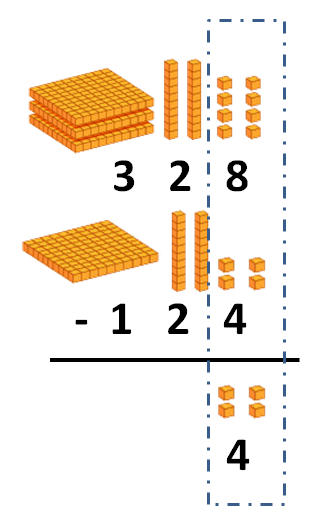
Y después la columna de las decenas:

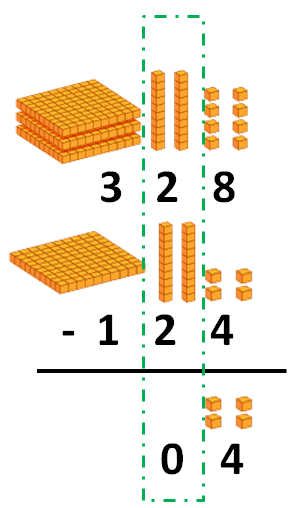
Y por último la columna de las centenas:

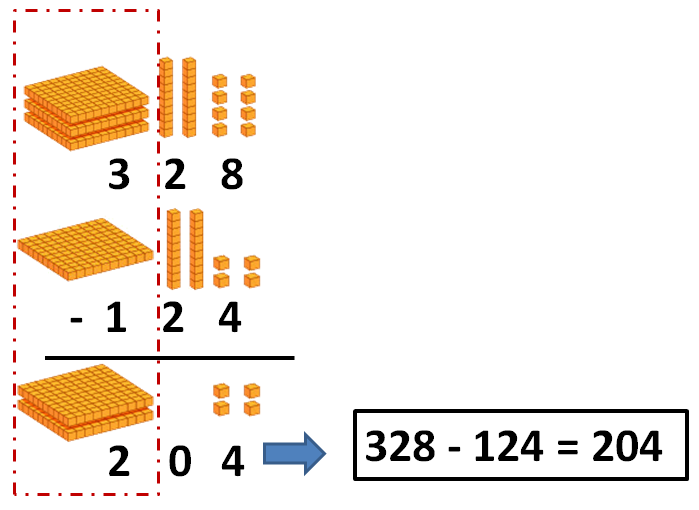
Y ¿qué pasa cuando en alguna columna no hay número? Pues hacemos lo mismo que antes: colocamos los términos desde la columna de las unidades hacia la izquierda, y restamos por columnas, empezando por las unidades. Para verlo mejor, vamos a resolver la segunda resta: 647 – 15

Primero la colocamos como hemos aprendido, y empezamos a restar por la columna de las unidades:

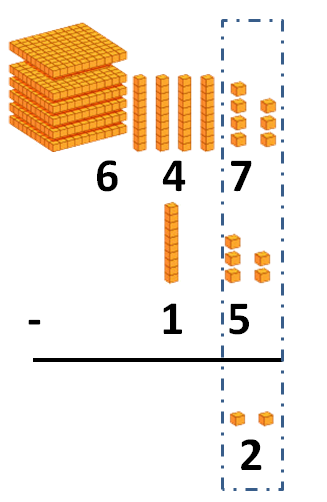
Y después la de las decenas:

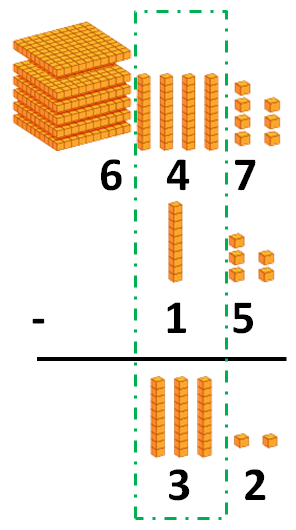
Por último, restamos en la columna de las centenas. Como el sustraendo tiene 0 centenas, el número de centenas sigue siendo el mismo:

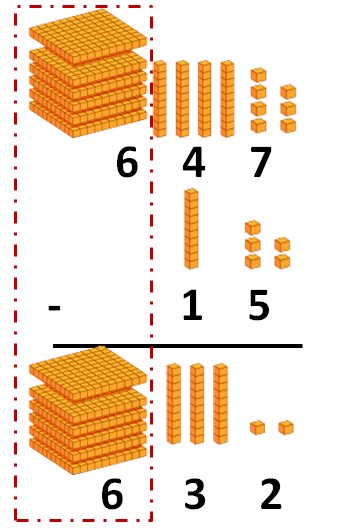
Aprender a restar con llevada

Cuando la cifra del minuendo es menor que la cifra del sustraendo tiene que pedir ayuda a la cifra del minuendo de la siguiente columna.

Por ejemplo:

Vamos a restar 32 – 17

Coloca el 17 debajo del 32 de manera que coincidan las unidades en la misma columna, es decir, el 7 y el 2.

Empieza restando la columna de las unidades:  2 – 7, pero como 2 es menor que 7  tienes que pedir ayuda a la siguiente columna. Esta columna se quita una decena (3 – 1) para dar 10 unidades (2 + 10).

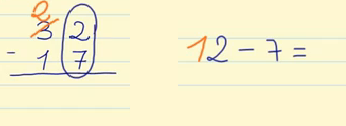
Ahora ya puedes restar  12 – 7 = 5

Resta la columna de las decenas:  2 – 1 = 1

Por lo tanto, el resultado de nuestra resta con llevada es  32 – 17 = 15

Estrategias para resolver sumas y restas en horizontal incompletas

vamos a ver algunas estrategias para resolver problemas en los que aparecen sumas y restas en horizontal incompletas. Para ello, nos ayudaremos de algunos ejemplos.

Adquirir unas estrategias de cálculo mental no siempre es fácil, ya que no hay un camino marcado por una guía y puede desesperar cuando no las consigues pronto.

Ten paciencia, verás como poco a poco vas añadiendo más a tu lista de estrategias y algún día, ésta se llena.

Ejemplo de resolución de una suma en horizontal incompleta

En primer lugar, veamos cómo resolver la siguiente suma incompleta:

Al observar el símbolo «+» y dos números, lo primero que puedes pensar que hay que hacer es sumar. ¡No te confundas! Lo que hay que hacer es buscar un número que, sumado a 86, de como resultado 756.

Como la operación inversa de la suma es la resta, ese número buscado será la resta de 756 y 86.

Puedes realizar esta resta descomponiendo los dos números de la manera que sea más fácil para ti. Aquí te muestro la mía:

• Como 756 y 86 tienen las mismas unidades, primero descompongo el 86 en 80 y 6. Así, resto primero 6 (que es más fácil) y luego 80:

• Ahora, como 750 tiene 5 decenas, separo el 80 en 50 y 30 para que sea más fácil restar, y resto primero 50 y después 30:

¡Ya tenemos el número buscado!

Como 756 – 86 = 670, entonces, 670 + 86 = 756, así que el número con el que podemos completar el hueco es 670.

Ejemplo de resolución de una resta en horizontal incompleta

Veamos ahora cómo resolver la siguiente resta incompleta: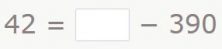

Como antes, al observar el símbolo «-» y dos números, lo primero que puedes pensar que hay que hacer es restar. Pero, si observas bien, verás que lo que hay que hacer es buscar un número que, si le restamos 390, de como resultado 42.

Como la operación inversa de la resta es la suma, ese número buscado será la suma de 390 y 42.

Nuevamente, puedes realizar esta suma descomponiendo los dos números de la manera que sea más fácil para ti. Aquí te muestro la mía:

Sumo primero las unidades, que es lo más sencillo. Así, descompongo el 42 en 40 y 2 y sumo:

Como 392 tiene 9 decenas, está a 1 decena de la siguiente centena, así que

descompongo el 40 en 10 y 30. Ahora, sumo primero 10 y después 30:

• 
  
• Esta suma es muy sencilla, ya que no coinciden centenas, decenas ni unidades en ambos números:

Hemos encontrado por fin el número buscado.

Como 390 + 42 = 432, entonces, 432 – 390 = 42, así que el número con el que podemos completar el hueco es 432.

¿Has visto que fácil resulta resolver problemas de sumas y restas en horizontal incompletas? Espero que estas estrategias te sirvan para ir añadiendo más a las que hayas ido adquiriendo a lo largo de tu vida.

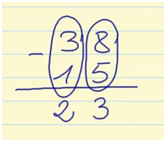
Pero recuerda que lo primero, antes de aplicarlas, es observar y pensar. Te animo a que resuelvas ahora tú la siguiente resta incompleta, que es algo distinta a las anteriores. Puedes dejar tu respuesta en los comentarios de este post: